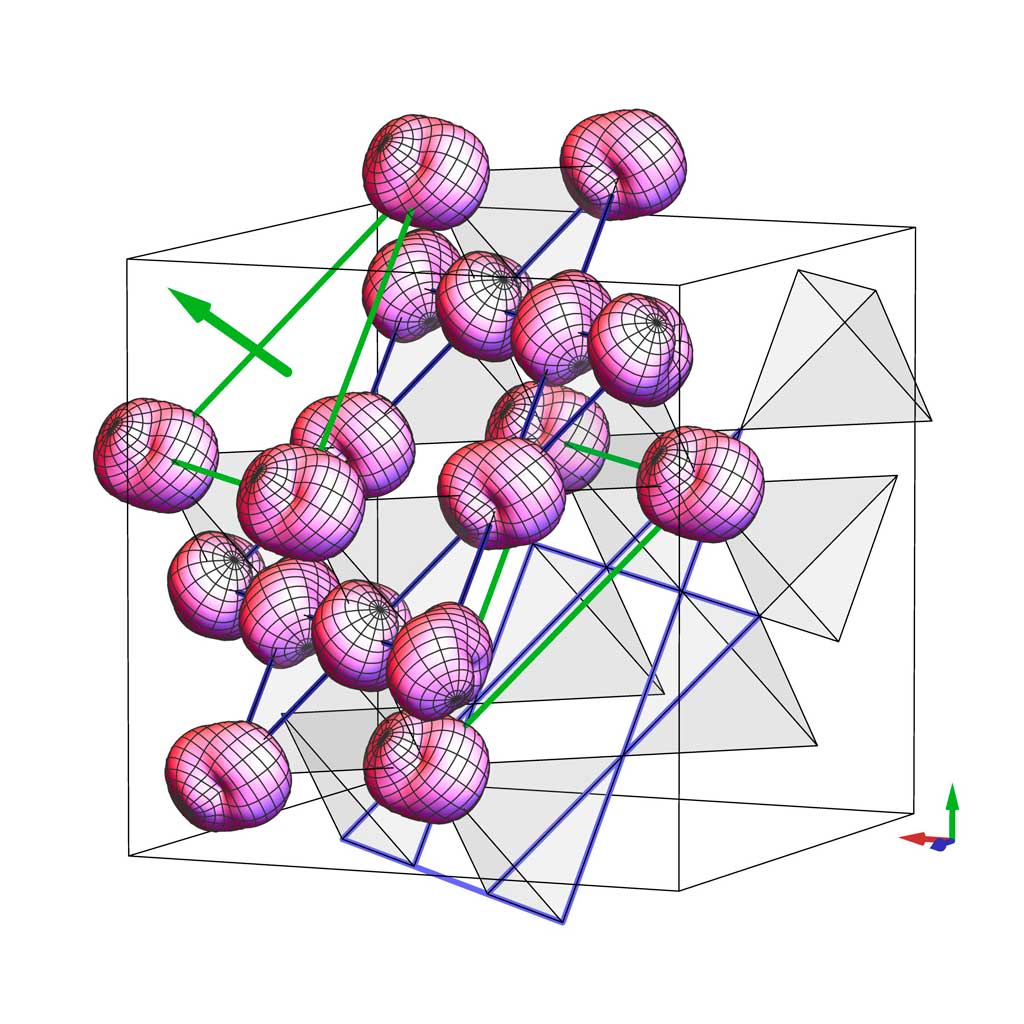
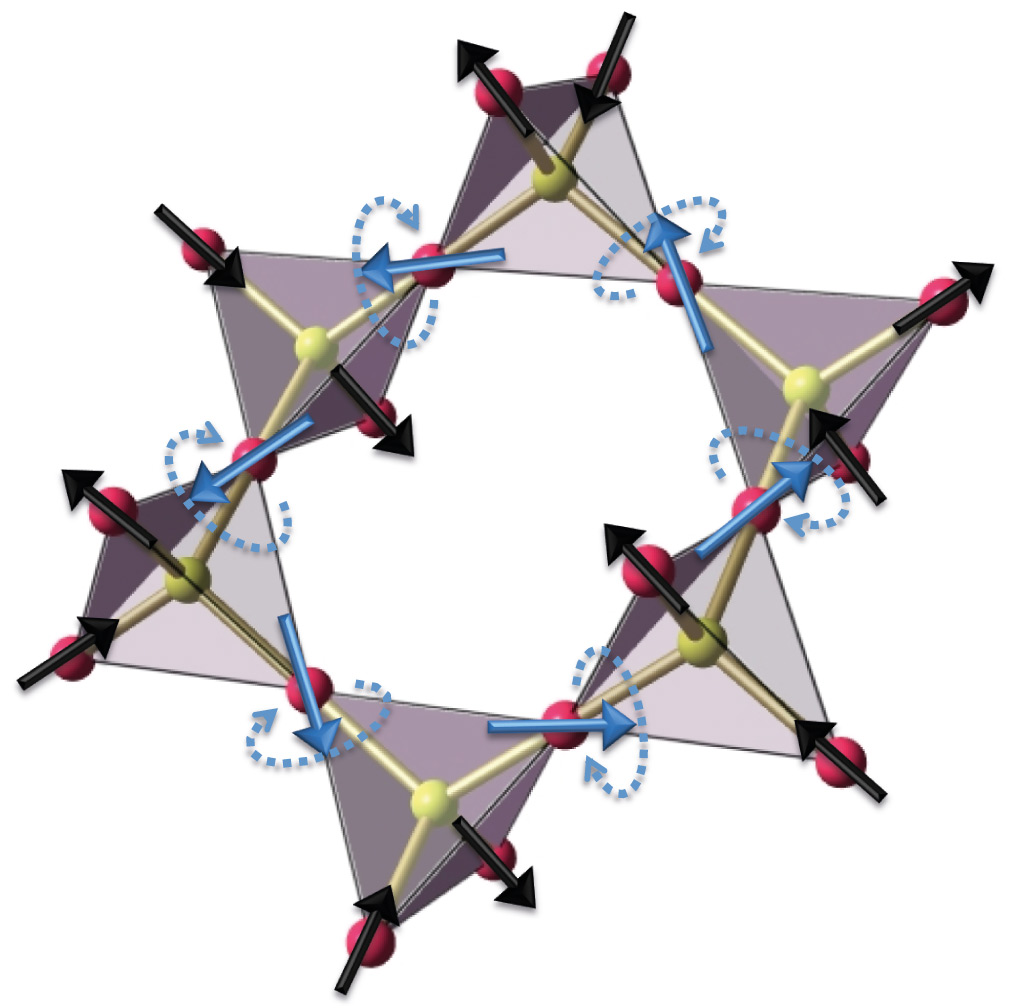
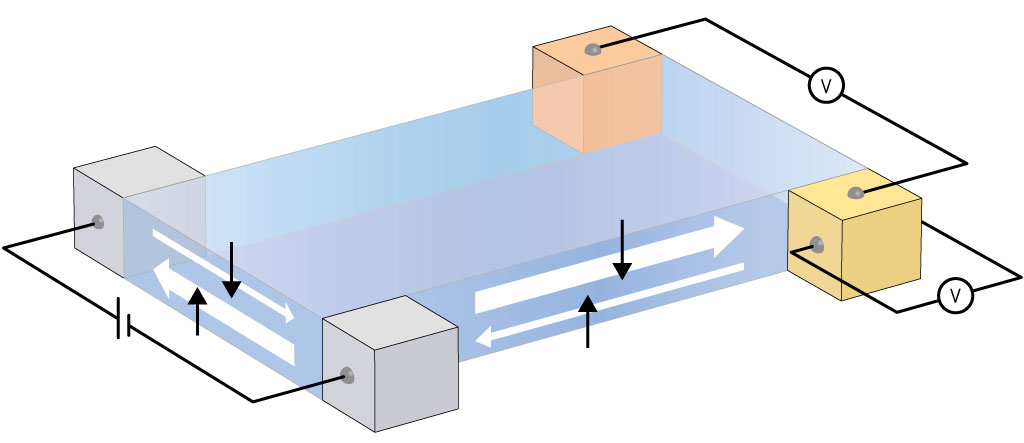
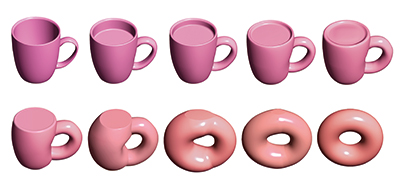We investigate novel quantum phases of many-electron systems in solids which emerge as a result of strong electron correlation and quantum effects. We theoretically study electronic properties of these new phases (such as transport and magnetism) and critical phenomena at phase transitions. Specifically, we study topological insulators and superconductors, frustrated quantum magnets, and other strongly correlated electron systems in transition metal oxides and molecular conductors, etc. We construct effective models for electrons in these materials and unveil their various emergent phases by solving quantum statistical mechanics of these models using both analytical and numerical methods.
Classifying topological insulators and topological superconductors
Modern electronics is based on the band theory that describes quantum mechanical motion of electrons in a solid. The band theory can explain properties of metals, insulators and semiconductors, and led to the invention of transistors. However, recent studies revealed some important physics which was missed in the standard band theory. Namely, electron wave functions can have a nontrivial topological structure in momentum space, and this leads to a topological insulator. In addition, superconductors with gapped quasiparticle excitations can be a topological superconductor. In principle there are various types of topological insulators (TIs) and topological superconductors (TSCs) in nature.
We constructed a general theory that can classify TIs and TSCs in terms of generic symmetries. This theory shows that in every spatial dimension there are three types of TIs/TSCs with an integer topological index and two types of TIs/TSCs with a binary topological index. We extend our theory to understand the effect of crystalline symmetry and electron correlation.
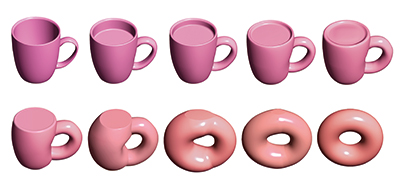
A coffee mug and a donut are equivalent in topology because they can be continuously deformed from one to the other. The wave functions of electrons in insulators can be topologically lassified.