Quantum geometric bounds for observables: Linear responses, Drude weight, and orbital magnetization
The quantum geometric tensor (QGT) provides nontrivial bounds among physical quantities, as exemplified by the metric-curvature inequality. We investigated various bounds for different observables through certain generalizations of the QGT. First, we demonstrate that bounds hold for all linear responses, which are produced by a QGT extended to many-body states, finite temperature, and general parameter space. As an application, we show the thermodynamic inequality originating from the convexity of free energy can be further tightened. Second, we establish a bound between the Drude weight and the orbital magnetization. This equality is exactly satisfied in the Landau level system, and systems with nearly flat bands tend to approach equality as well. We apply the resulting inequality to two orbital ferromagnets and support that the twisted bilayer graphene system is close to the Landau level system. Moreover, we show that an analogous inequality also holds for a higher-order multipole, magnetic quadrupole. Finally, we discuss the analogy between the QGT and the uncertainty principle, emphasizing that the existence of nontrivial bounds necessarily reflects quantum effects.

The relation between the flatness of the band (inset) and the inequality between the Chern number and determinant of the quantum metric tensor G. The inequality is almost saturated when the band becomes flat. DOI: https://doi.org/10.1103/qxbl-qd4f
Phonon Thermal Hall Effect in Mott Insulators via Skew Scattering by the Scalar Spin Chirality
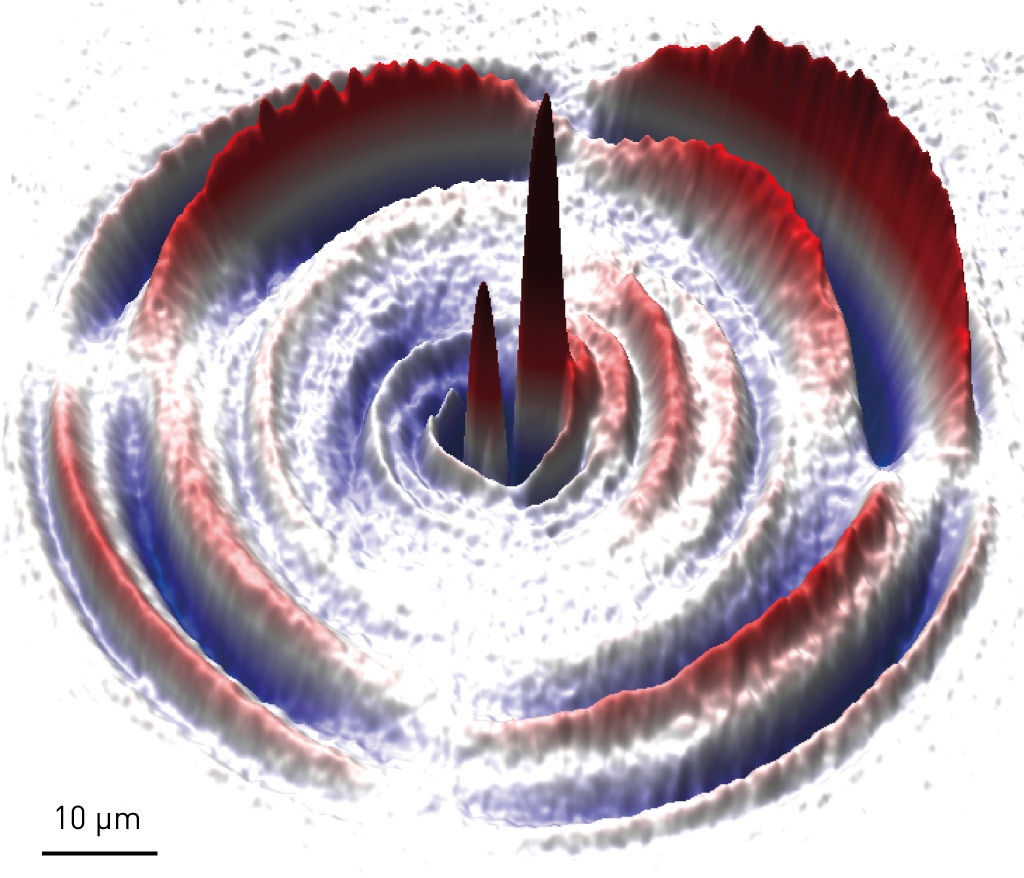
Thermal transport is a crucial probe for studying excitations in insulators. In Mott insulators, the primary candidates for heat carriers are spins and phonons; which of these candidates dominates the thermal conductivity is a persistent issue. Typically, phonons dominate the longitudinal thermal conductivity while the thermal Hall effect (THE) is primarily associated with spins, requiring time-reversal symmetry breaking. The coupling between phonons and spins usually depends on spin-orbit interactions and is relatively weak. Here, we propose a new mechanism for this coupling and the associated THE: the skew scattering of phonons via spin fluctuations by the scalar spin chirality. This coupling does not require spin-orbit interactions and is ubiquitous in Mott insulators, leading to a thermal Hall angle on the order of 10−3 to 10−2. Based on this mechanism, we investigate the THE in YMnO3 with a trimerized triangular lattice where the THE beyond spins was recognized, and we predict the THE in the kagome and square lattices.

Phonon scattering due to fluctuations of scalar spin chirality in Mott insulators. This scattering mechanism causes scattering in the opposite transverse directions, depending on the direction of the phonon angular momentum, resulting in the thermal Hall effect.
Thermal Hall effects due to topological spin fluctuations in YMnO3
The thermal Hall effect in magnetic insulators has been considered a powerful tool to study the topological nature of charge-neutral quasiparticles such as phonons and magnons. Yet, unlike the kagome system, the triangular lattice has received less attention for studying the thermal Hall effect because the scalar spin chirality cancels out between adjacent triangles. However, such cancellation is violated when the triangular lattice is distorted, i.e., trimerized triangular lattice. We report that the trimerized triangular lattice of multiferroic hexagonal manganite YMnO3 produces a highly unusual thermal Hall effect under an applied magnetic field. Our theoretical calculations demonstrate that the thermal Hall conductivity is related to the splitting of the otherwise degenerate two fluctuating chiralities of its 120° magnetic structure. Our result is one of the most unusual cases of topological physics due to this broken Z2 symmetry of the chirality in the supposedly paramagnetic state of YMnO3, due to strong topological spin fluctuations with the Dzyaloshinskii-Moriya interaction.

(Left) Crystal structure and spin structure of magnetic ferroelectrics YMnO3. (Right) Comparison of the calculation results of the thermal Hall effect by numerical simulation for the spin Hamiltonian and the experimental results. Theories are shown in blue, and experiments are shown in red and persimmon.
Ha-Leem Kim et al., “Thermal Hall effects due to topological spin fluctuations in YMnO3”, Nature Communications 15, 243 (2024). https://doi.org/10.1038/s41467-023-44448-9
Shift current by phonon excitation in ferroelectrics
The shift current induced under light irradiation in crystals without inversion symmetry is a current due to quantum geometry, which is essentially different from the normal transport current. Therefore, it may be possible to induce a direct current without generating photocarriers. Specifically, there is a process in which real excitation of phonons occurs by light irradiation in an energy region lower than the bandgap and, at the same time, direct current is generated through virtual electron-hole pairs. This possibility is expected to be applied to photodetectors in the terahertz region, and is extremely interesting from the viewpoint of fundamental physics. Using the Feynman diagram method, we formulated the nonlinear optical conductivity that expresses this process, and based on the derived formula, we performed model calculations and first-principles band calculations. As a result, it is found that the shift current is comparable between the actual interband transition with photon energy of eV order and the phonon excitation with photon energy of about 10 meV order. These theoretical calculations were compared with experimental observations and semi-quantitative agreement was obtained. In particular, the DC current is almost independent of the external bias voltage, indicating no photocarrier generation.

(Left) Feynman diagram of the shift current due to phonons. (Right) Nonlinear optical response function by first-principles calculation. A is for the low-energy region corresponding to phonon excitation, and B is for the visible-light region corresponding to electronic excitation. Y.Okamura et al., “Photovoltaic effect by soft phonon excitation”, Proc. Nat. Acad. Sci., 119(14), e2122313119 (2022). https://doi.org/10.1073/pnas.2122313119
Theory of quantum geometry in optical responses
The optical response is not only basic in the properties of matter, but also important from the viewpoint of application. It was beginning to be recognized that this optical response was deeply related to the geometrical properties of the wave function, but the whole picture was not clear. We find that linear response, second-order nonlinear response, and third-order nonlinear response correspond to each of metric, connection, and curvature in non-Euclidean Riemannian geometry, and succeeded to construct a general theoretical framework. Then, as a specific application thereof, we have studied the photo-induced Hall effect, which is a third-order nonlinear optical response, in the surface state of the magnetic topological insulator, and find that the term expressed by the Riemann curvature becomes dominant at the band edge.

(Left figure) Schematic band structure of the surface state of magnetic topological insulator. (Right figure) Photon energy dependence of the photocurrent for the circularly polarized light. Near the edge of the band gap, the K-term which is closely related to the Riemannian curvature, i.e., the geometric quantity of the wavefunction, is dominant over the other terms. J. Ahn, G.Y. Guo, N.Nagaosa, A. Vishwanath, A “Riemannian geometry of resonant optical responses”, Nature Physics 18, 290 (2022)
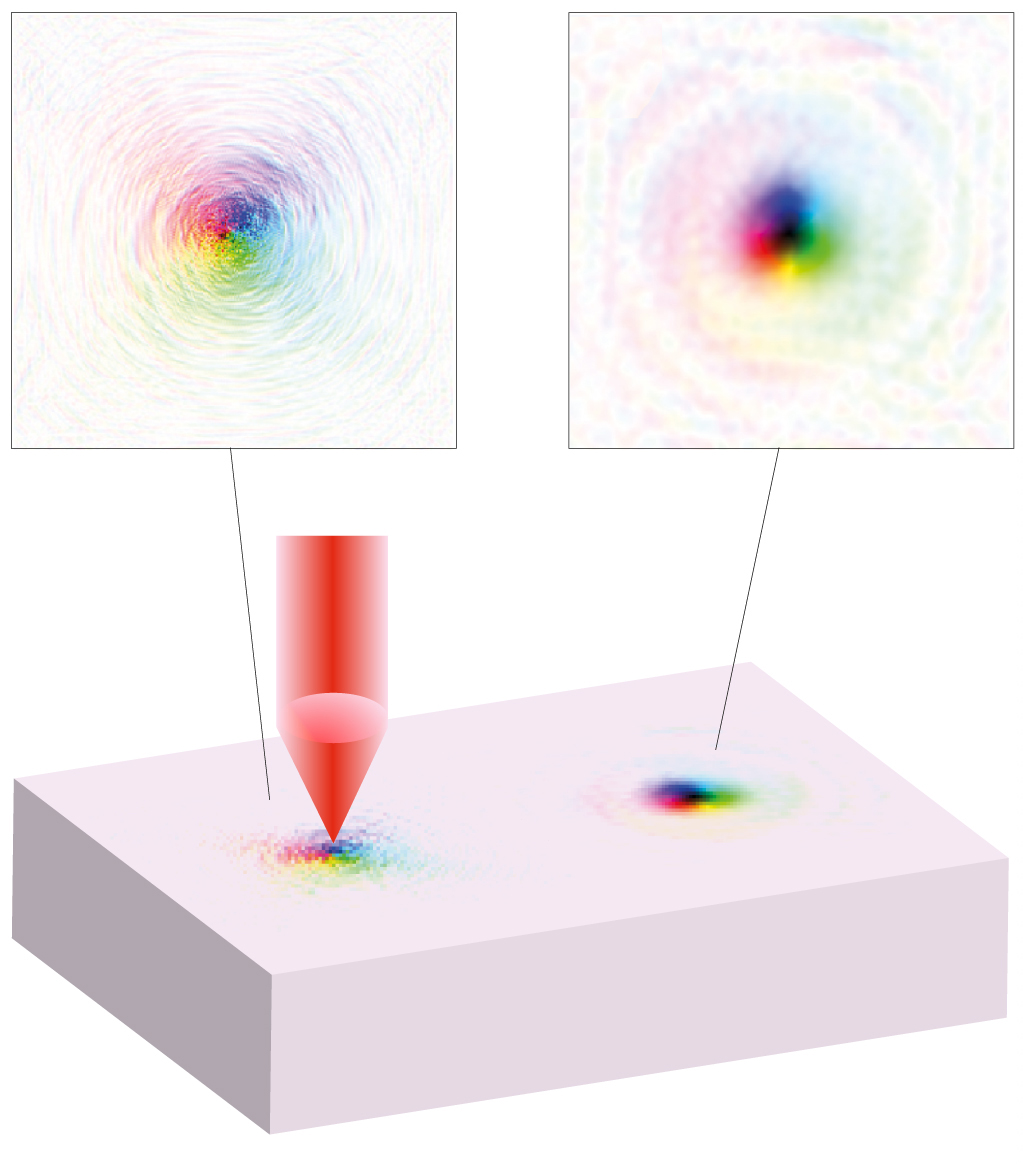
Theory of shift current in Anderson insulator
The shift current induced under light irradiation in a crystal without inversion symmetry is a current due to quantum geometry that is essentially different from the normal transport current. Therefore, it is expected that the tolerance to the Anderson localization effect due to the disorder will be significantly different. If only the transport current by the optical carrier is suppressed, it will lead to the improvement of the efficiency of the solar cell and the suppression of the noise in photodetector, so it has been recognized as an important problem in application. For a one-dimensional Anderson insulator model, the shift current is calculated by the Keldysh non-equilibrium Green’s function method. We have found that, when the disorder strength is moderate and the dissipation due to electron-phonon interaction is included, the magnitude of the shift current hardly depends on the localization length. This is a behavior that is completely different from the transport current. It was found that when the disorder is further strengthened to exceed the energy gap, the conduction band and the valence band are mixed, so that the shift current also decreases.

(Left figure) Conceptual diagram of shift current in Anderson insulator. (Right figure) The disorder strength (Vmd) dependence of the shift current. Up to Vmd = 0.5, the shift current hardly changes even though the wave function is already localized. If the disorder is further strengthened, the shift current will also decrease due to the mixing between the bands.
H. Ishizuka and N. Nagaosa, “Theory of bulk photovoltaic effect in Anderson insulator ”, Proc. Nat. Acad. Sci., 118(10) e2023642118 (2021).
Theory of emergent inductor
The emergent electric and magnetic fields originate from the Berry phase associated with the spin direction n. While the emergent magnetic field is detected as the topological Hall effect, the emergent electric field is given by the dynamics of the spin structures and can be detected as the voltage drop.
For the current-driven motion of the spiral spin structure, we find that the emergent electric field and the consequent voltage drop are proportional to the time-derivative of the current density, corresponding to the inductance given by
where A and ℓ are the cross-section and length of the sample, λ the period of the spiral, jint is related to the magnetic anisotropy energy, and γ is a constant of the oder of unity. This emergent inductor does not require any complex structures such as coil and core, and the inductance is inversely proportoinal to the cross section of the sample. Therefore, it is advantageous for the miniturization of the devices.

(Left) Principles of emergent inductor. The spin structure of spiral magnet (upper), and the modification of the spin structure under the current-driven motion (lower). When the translational motion X occurs, the spins are tilted by the angle f. When ac current is applied, the voltage drop along the direction of the wavevector is induced proportional to the time-derivative of the current density. (Right) Various spin structures showing the inductance.
N. Nagaosa, “Emergent inductor by spiral magnets”, Japanese Journal of Applied Physics, 58(12) 12909 (2019)
Theory of shift current in noncentrosymmetric materials
It has been known that the dc current is induced by the photo-excitation without the external electric field in noncentrosymmetric materials. This phenomenon, called ”shift current”, is driven by the geometrical Berry phase of the Bloch electrons in solids, and is one of the topological currents. We have studied theoretically the physical properties of this shift current such as the effects of the relaxation due to impurity scattering and electron-phonon interaction, the acceleration by external electric field, and quantum shot noise of shift current. We have revealed the followings: (i) the relaxation affects the dependence of the shift current on the intensity of photo-excitation, while shift current does not depend on it when the photo-excitation is weak. (ii) I-V characteristics of the shift current under the external electric field depends strongly on the relaxation, and the lower mobility of the photo-carriers gives the higher energy-conversion ratio, which is in sharp contrast to the conventional case. (iii) The noise of the shift current is reduced when the band-width is small. In addition, we have estimated the shift current in SbSI, and obtained the good agreement with the experimental result quantitatively including the energy dependence of the incident light.

Shift current in ferroelectric semiconductor SbSI. Left: Crystal structure of SbSI. Middle: Time dependence of the emitted THz light. Right: The incident-light energy dependence of the shift current. Theory and experiment shows good agreement quantitatively.
M. Sotome, et al., “Spectral dynamics of shift current in ferroelectric semiconductor SbSI” Proceedings of National Academy of Sciences of the United States of America 116, 1929-1933 (2019)
Skyrmion dynamics in disordered magnet
Distinct from the magnetic textures such as domain wall, helical structure, and vortex, the topological particle in magnets, skyrmion, has unique features. A typical one is the extremely small critical current density jc for the current-driven motion of the skyrmion. The finite jc indicates the pinning effect due to the disorder such as impurities and defects. We study the current-driven skyrmion dynamics with disorders by a numerical simulation of Landau-Lifshitz-Gilbert equation, and four different skyrmion phases are found: (A) pinned state, (B) depinned state, (C) skyrmion multiplication/annihilation, and (D) segregation of skyrmions, as the current density increases, while only two phases (A) and (B) appear in the weak disorder case. The new phases (C) and (D) are due to the deformation of skyrmions and spin wave emission, respectively. In addition, we have developed the replica field theory of skyrmion glass state, and revealed the dramatic differences between helical and skyrmion phases by calculating the physical properties such as domain size, pinning frequency, nonreciprocal collective modes, optical conductivity, and magnetic resonance.

Skyrmion multiplication
Due to the strong impurity effect, the current driven skyrmion splits into two or more.
W. Koshibae and N. Nagaosa, Scientific Reports 8, 6328 (2018)