モット絶縁体におけるスカラースピンカイラリティによるスキュー散乱を介したフォノン熱ホール効果
熱伝導は、絶縁体の励起を研究する上で極めて重要なプローブである。モット絶縁体では、熱伝導体の主要な候補はスピンとフォノンであり、これらの候補のどちらが熱伝導率を支配するかは長年の懸案である。一般的に、フォノンは縦方向の熱伝導率を支配する一方、熱ホール効果(THE)は主にスピンに関連し、時間反転対称性の破れを必要とすると考えられてきた。フォノンとスピンの結合は通常スピン軌道相互作用に依存し、比較的弱い。ここでは、この結合とそれに伴うTHEの新しい機構を提案する。それは、スカラースピンカイラリティによるスピン揺らぎを介したフォノンのスキュー散乱である。この結合はスピン軌道相互作用を必要とせず、モット絶縁体において普遍的であり、10-3から10-2のオーダーの熱ホール角をもたらす。このメカニズムに基づき、スピンだけでは説明できないTHEが観測された、三量体化した三角格子を持つYMnO3におけるTHEを解析し、さらにカゴメ格子と正方格子におけるTHEを予測した。

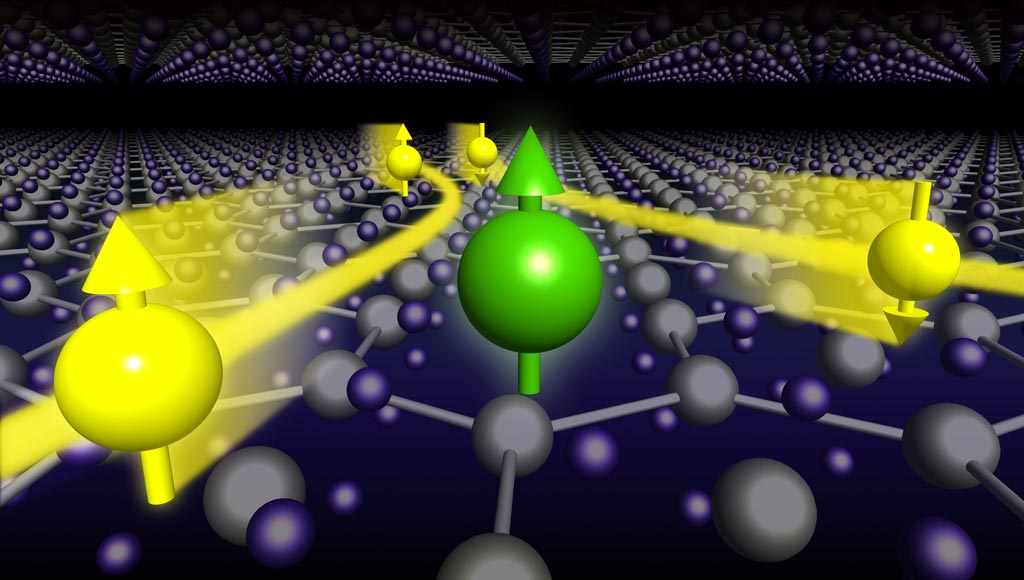
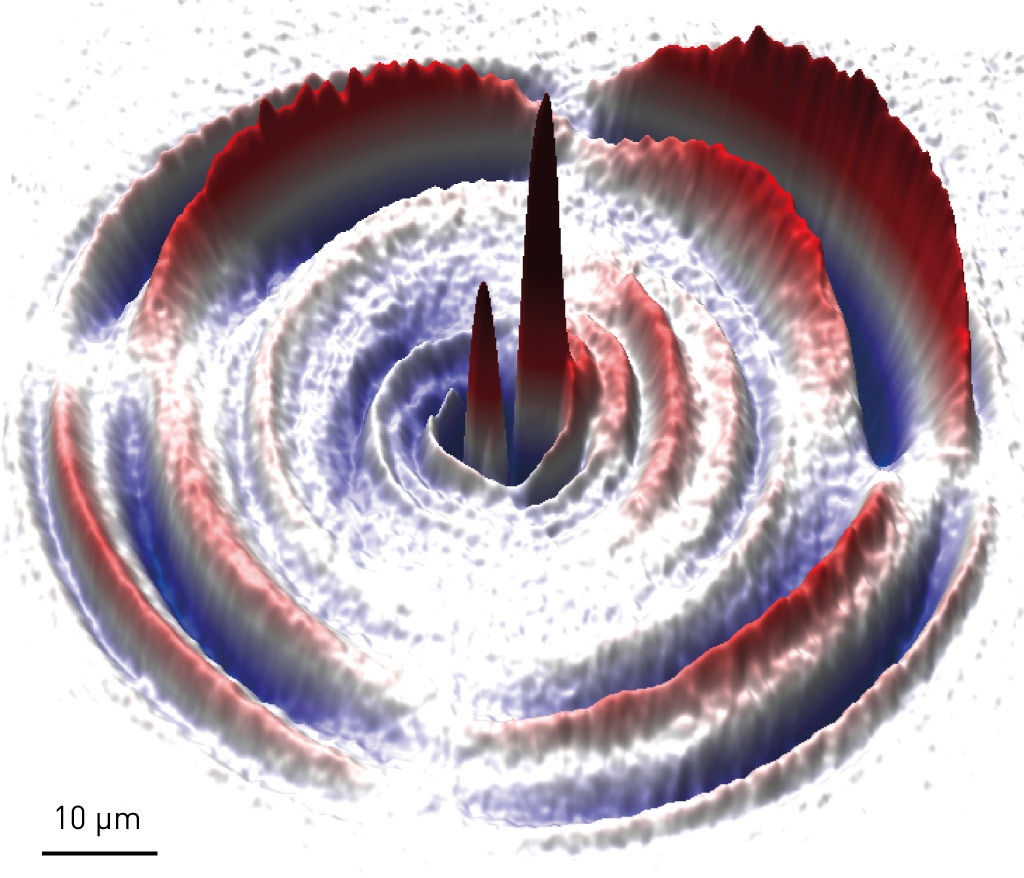
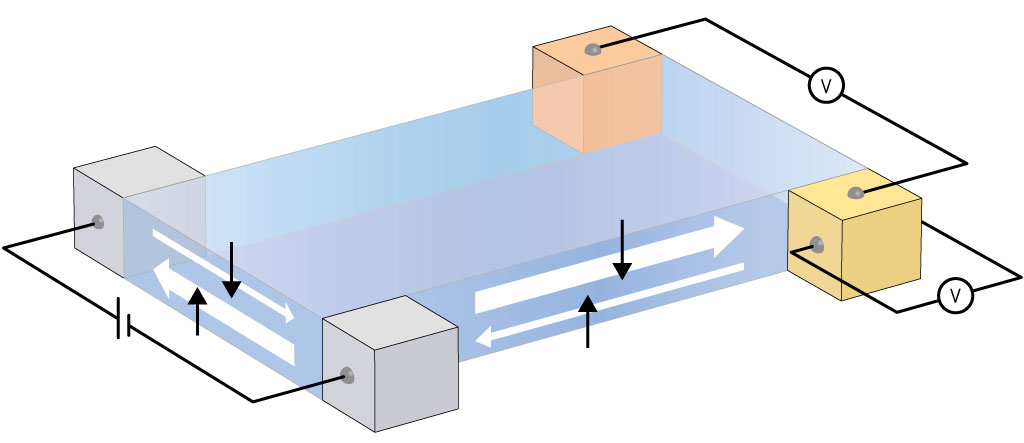
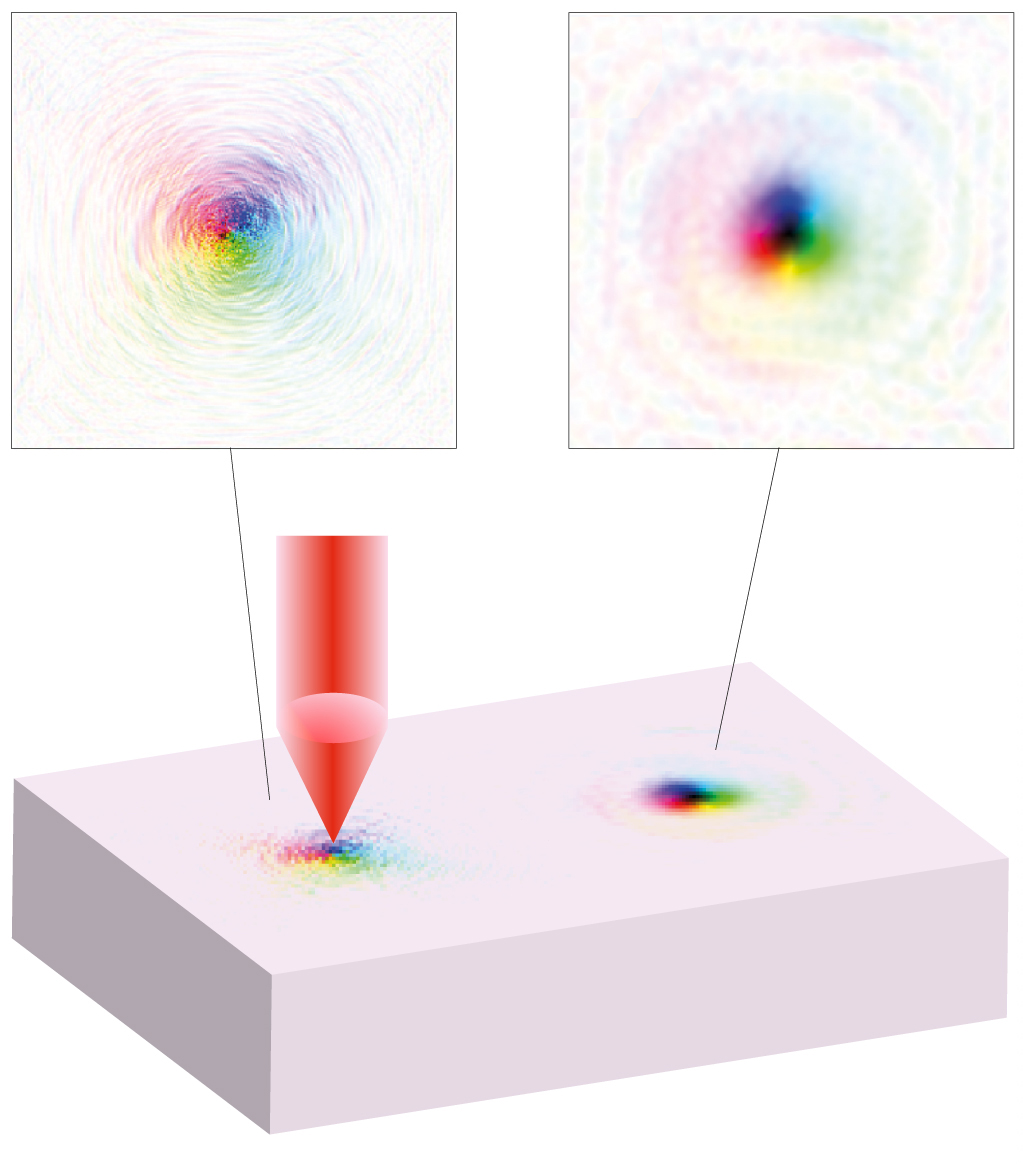
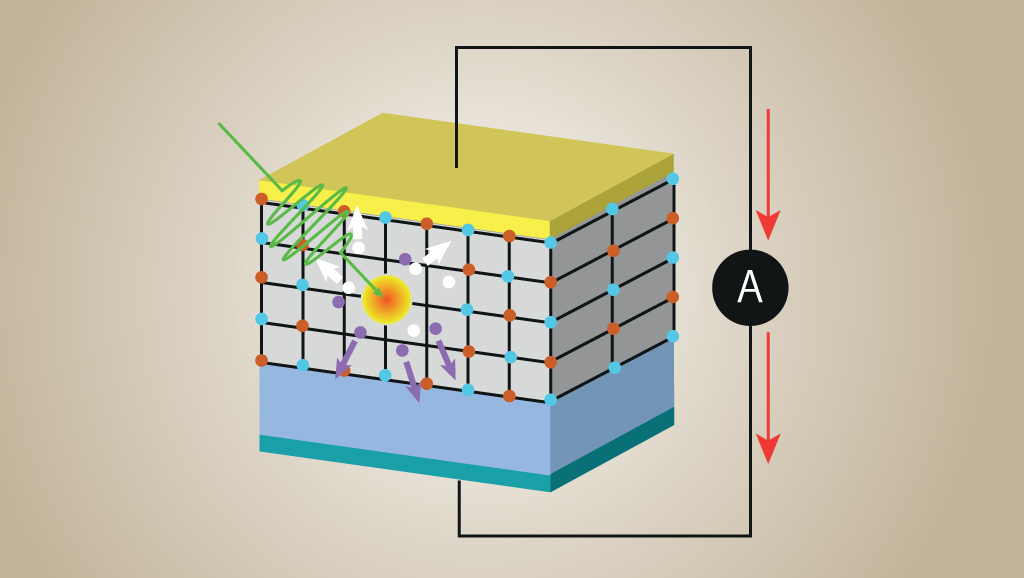
モット絶縁体におけるスカラースピンカイラリティの揺らぎによるフォノン散乱。この散乱機構によって、フォノンの角運動量の方向に応じて逆向きの横方向へと散乱が起こり、熱ホール効果が生じる。
YMnO3におけるトポロジカルなスピン揺らぎによる熱ホール効果
磁気絶縁体における熱ホール効果は、フォノンやマグノンのような電荷中性の準粒子のトポロジカルな性質を調べる強力な方法と考えられてきた。しかし、カゴメ格子系とは異なり、三角格子は熱ホール効果の研究対象としてあまり注目されてこなかった。スピンのキラリティが隣接する三角形間で相殺されるためである。しかし、三角格子が歪んでいると、このような打ち消しは完全ではなく、スピンキラリティによる熱ホール効果が期待される。我々はマルチフェロイック六方晶マンガン酸化物YMnO3の三量体化した三角格子が、磁場印加下で熱ホール効果を発生することを見出した。我々の理論計算により、熱ホール伝導度は、120°磁化構造の2つのキラル性の分裂に関係していることを明らかにした。この結果はトポロジカル物理学の最も珍しいケースの一つであるYMnO3が、Dzyaloshinskii-Moriya相互作用の存在下でのトポロジカルな強いスピン揺らぎによって熱ホール効果を示すことを明らかにした。

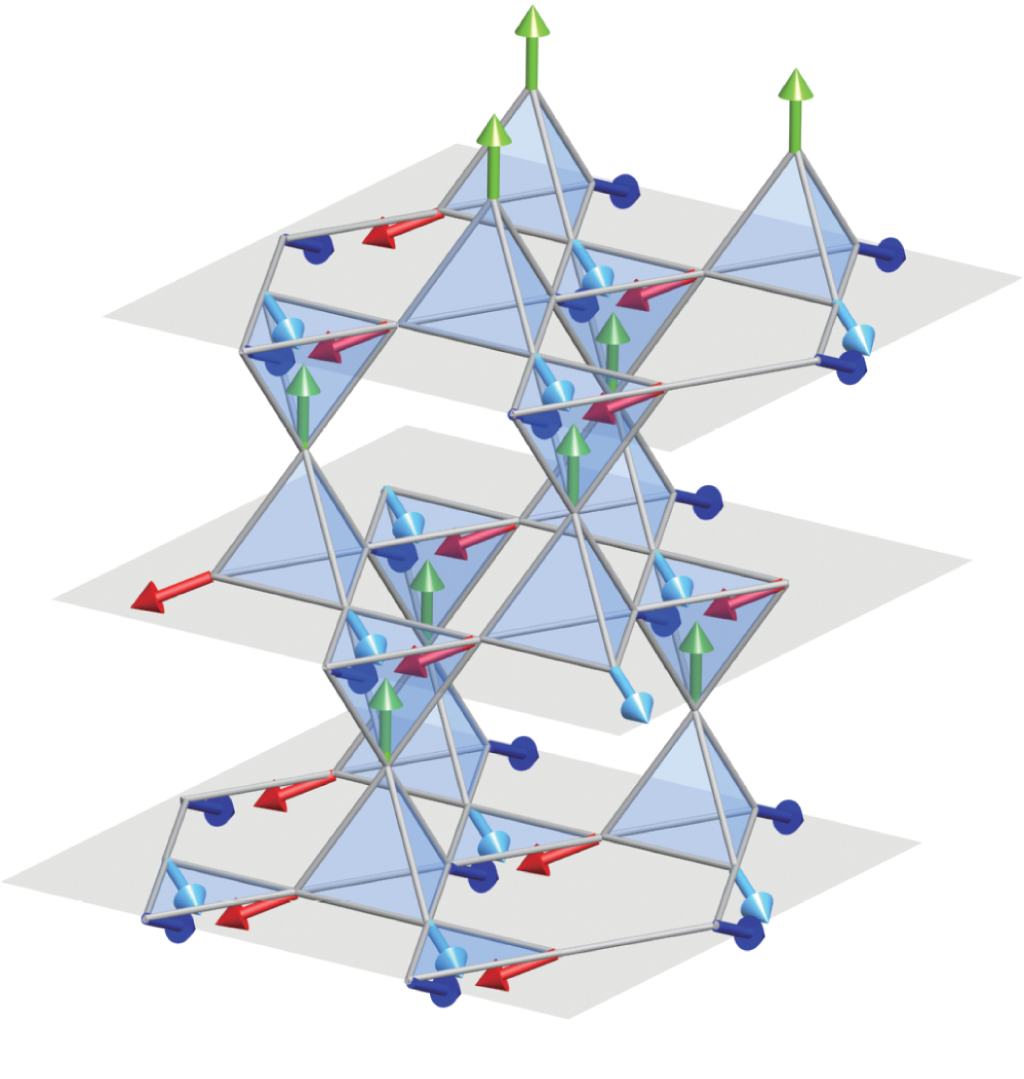
(左図)YMnO3の結晶構造とスピン構造。(右図)スピンハミルトニアンに対する数値シミュレーションによる熱ホール効果の計算結果と実験結果の比較。理論は青、実験は赤と柿色で示す。Ha-Leem Kim et al., “Thermal Hall effects due to topological spin fluctuations in YMnO3”, Nature Communications 15, 243 (2024). https://doi.org/10.1038/s41467-023-44448-9
強誘電体におけるフォノン励起によるシフト電流
反転対称性を持たない結晶において光照射下で誘起されるシフト電流は通常の輸送電流とは本質的に異なる量子幾何学による電流である。従って、光キャリアを生成することなく直流電流を誘起できる可能性がある。具体的には、バンドギャップよりも低いエネルギー領域の光照射によってフォノンを実励起し、同時に仮想的な電子・正孔対を介して直流電流を生成する過程が存在する。この可能性はテラヘルツ領域の光検出器への応用も期待されるとともに、基礎物理学の観点からも極めて興味深い。我々は、ファインマン ダイアグラム法を用いて、この過程を表す非線形光学伝導度を定式化し、そこから導き出された公式に基づいて、モデル計算と第一原理バンド計算による評価を行った。その結果、シフトカレントはeVオーダの光子エネルギーを持つ実際のバンド間遷移の場合と、約10 meVオーダのフォノンエネルギーでのフォノン励起の場合との間で同程度であることが分かった。これらの理論計算を実験観測と比較し、半定量的な一致が得られた。特に、直流電流は外部バイアス電圧にほとんど依存せず、フォトキャリアの生成がないことを示している。

(左図)フォノンによるシフトカレントのファインマンダイアグラム。(右図)第一原理計算による非線形光学応答関数。Aはフォノン励起に対応する低エネルギー領域、 Bは電子励起に対応する可視光領域の結果を示す。 Y.Okamura et al., “Photovoltaic effect by soft phonon excitation”, Proc. Nat. Acad. Sci., 119(14), e2122313119 (2022). https://doi.org/10.1073/pnas.2122313119
光学応答における量子幾何学
光学応答は物質の性質の中でも基本的であるばかりではなく、応用の観点からも重要である。この光学応答と、波動関数の持つ幾何学的な性質が深く関係していることが認識され始めていたが、その全貌は明らかではなかった。我々は、線形応答、2次の非線形応答、3次の非線形応答がそれぞれ非ユークリッド・リーマン幾何学における、メトリック、接続、曲率のそれぞれに対応することを見出し、一般性を持つ理論的枠組みを構築することに成功した。そして、その具体的な応用として、磁性トポロジカル絶縁体の表面状態における3次の非線形光学応答である光誘起ホール効果を計算し、そのバンド端においてはリーマン曲率で表現される項が支配的になることを示した。

(左図)磁性トポロジカル絶縁体のバンド構造。(右図)円偏光に対する光電流のフォトンエネルギー依存性。K termは波動関数の幾何学的な量であるリーマン曲率と直接関係した部分であり、ギャップの直上で支配的な寄与をする。J. Ahn, G.Y. Guo, N.Nagaosa, A. Vishwanath, A “Riemannian geometry of resonant optical responses”, Nature Physics 18, 290 (2022).
Anderson絶縁体におけるシフト電流
反転対称性を持たない結晶において光照射下で誘起されるシフト電流は通常の輸送電流とは本質的に異なる量子幾何学による電流である。従って、乱れによるアンダーソン局在効果に対する耐性も大きく異なることが期待される。光キャリアによる輸送電流だけが抑えられれば、太陽電池の効率向上と光検出器の雑音抑制につながるために、応用上も重要な問題として認識されていた。1次元アンダーソン絶縁体のモデルに対し、Keldysh非平衡Green関数法でシフトカレントを計算し、その結果、乱れが中程度までの強さであれば、電子格子相互作用による散逸を入れた場合には、シフト電流の大きさは局在長にほとんど依らないことが示された。これは、輸送電流とは全く異なる振る舞いである。さらに乱れをエネルギーギャップを超えるまで強くすると、伝導帯と価電子帯が混じってしまうために、シフト電流も減少することが分かった。

(左図)アンダーソン絶縁体におけるシフト電流の概念図。(右図)シフト電流の乱れの強さVmd依存性。Vmd=0.5ではすでに波動関数は局在しているにも関わらずシフト電流はほとんど変化しない。さらに乱れを強くするとバンド間の混じりによってシフト電流も減少する。
H. Ishizuka and N.Nagaosa, “Theory of bulk photovoltaic effect in Anderson insulator ”, Proc. Nat. Acad. Sci., 118(10) e2023642118 (2021).
創発インダクターの理論
磁性体における非共線スピン構造には量子力学的なベリー位相が付随しており、それがベクトルポテンシャルとして電子系に働くことで、創発電磁場を発生する。このうち創発磁場はトポロジカルホール効果として観測されるが、スピンが時間依存性を持つ場合には創発電磁誘導によって創発電場が発生する。この創発電場は電圧降下として実際に観測される。らせん磁性体におけるスピン構造の運動を考えると、創発電場は電流密度の時間微分に比例する値が得られる。これは、次式で与えられるインダクタンスに相当する。 ここで、Aは断面積、ℓ は試料長、λ はらせんの周期、jintは磁気異方性に関係した量でγ は1オーダーの定数である。創発インダクターはコイルや鉄心などの構造を必要とせず、かつインダクタンスが断面積に逆比例する。これらの性質は、らせん磁性体がインダクターの微細化に有利なことを示している。
ここで、Aは断面積、ℓ は試料長、λ はらせんの周期、jintは磁気異方性に関係した量でγ は1オーダーの定数である。創発インダクターはコイルや鉄心などの構造を必要とせず、かつインダクタンスが断面積に逆比例する。これらの性質は、らせん磁性体がインダクターの微細化に有利なことを示している。

(左図)らせん磁性体におけるスピン構造(上)と、その電流に対する運動と変形(下)。らせん構造が併進運動するとスピンが回転面から角度φだけ起き上がる。この運動が交流電流によって駆動されると、電流の時間微分に比例した電圧がらせんの波数方向に生じる。(右図)創発インダクターの候補である様々なスピン構造。
N. Nagaosa, “Emergent inductor by spiral magnets”, Japanese Journal of Applied Physics, 58(12) 12909 (2019)
反転対称性を持たない物質におけるシフトカレントの理論
反転対称性を持たない物質に光を照射すると、外部電界なしに直流の光電流が流れることが知られている。この現象―シフトカレントーは固体中電子のベリー位相という幾何学的構造によって駆動される「トポロジカルカレント」の一種である。我々は、この固体中には不純物散乱や電子格子相互作用による電子緩和の効果や、外部電界下での光キャリアの加速、光電流のノイズ、などシフトカレントの物理的性質を理論的に研究した。その結果、緩和の効果は光強度依存性に現れ、光強度が小さい時にはシフトカレントは緩和に依存しないこと、しかし電界下でのI-V特性は緩和依存性が大きく、易動度が小さいほどエネルギー変換効率が大きくなるという、従来の光電流とは正反対の振る舞いを見出した。また、光電流のノイズは、バンド幅が小さい時に小さくなることを明らかにした。さらに、第一原理計算によって強誘電半導体SbSIのシフトカレントを計算し、実験とその励起エネルギー依存性も含めて定量的な一致を得た。

強誘電半導体SbSIのシフトカレント。左図:SbSIの結晶構造。中:テラヘルツ光強度の時間依存性。右:シフトカレントの入射光エネルギー依存性と理論計算との比較。定量的な一致が得られている。
M. Sotome, et al., “Spectral dynamics of shift current in ferroelectric semiconductor SbSI” Proceedings of National Academy of Sciences of the United States of America 116, 1929-1933 (2019)
不純物系におけるskyrmionのダイナミクス
らせん磁気構造や磁壁そして磁気渦と異なる、トポロジカルな磁気粒子skyrmionは、様々の特性をもつ。極めて小さな電流により駆動できる運動特性はその典型である。一方で、多結晶材料などにおいて不純物効果が強くなれば、skyrmionはまた、多様な運動形態を示す。我々はLandau-Lifshitz-Gilbert方程式を用いた数値シミュレーション法により、不純物効果の強い系における電流駆動skyrmionのダイナミクスを調べた。そして次のようなskyrmion集団の動的振る舞いを見出した: 印可電流の増加とともに、(A) ピン止め状態、 (B) ピン止めが外れた状態、 (C) skyrmion の増殖/消滅現象、そして (D) skyrmionの凝集現象が出現する。これらのうち (C) の増殖現象は、強く歪んだskyrmionの分裂に起因する。また (D) の凝集現象は不純物に散乱されるskyrmionが放つスピン波が、skyrmion間の引力を媒介することによる。また、レプリカ場の理論を用いた解析的手法で、スキルミオングラス状態を記述する理論を構築し、ピン止め周波数、ドメインサイズ、非相反スピン集団励起モード、光学応答、磁気共鳴、などの物性に対する予言を行い、ヘリカル相との顕著な相違を明らかにした。

電流駆動skyrmion増殖の素過程
強い不純物効果により、電流駆動skyrmionは歪み、分裂する。
W. Koshibae and N. Nagaosa, Scientific Reports 8, 6328 (2018).