Topological Quantum Matter Research Unit

Non-coplanar helimagnetism in the layered van-der-Waals metal DyTe₃

Van-der-Waals magnets with highly anisotropic chemical bonding can be exfoliated to realize ultrathin sheets or interfaces. With an eye towards future applications in twistronics, however, the lack of lattice-incommensurate helimagnets within this material class is a particular problem. Via polarized neutron scattering, we reveal the cycloidal, or conical, magnetic structure in DyTe₃, and establish a spin Hamiltonian that captures the coupling of magnetic moments and an underlying charge density wave (CDW). Experimentally, we find two coupled order parameters: q_AFM = (0 1 0.5) signifies uudd AFM coupling along the c-axis, while q_cyc = (0 0 0.207) corresponds to a superimposed cycloidal component, indicating coupled charge and spin density wave orders. Furthermore, we identify a structural feature of this material class as a key driver of helimagnetism: The mixed covalent / metallic crystal field environment of Dy³⁺ ions both suppresses magnetic anisotropy and enables strong coupling between magnetic moments and the charge-density wave order. Our work paves the way for twistronics research, where helimagnetic layers can be combined to form complex spin textures on-demand.

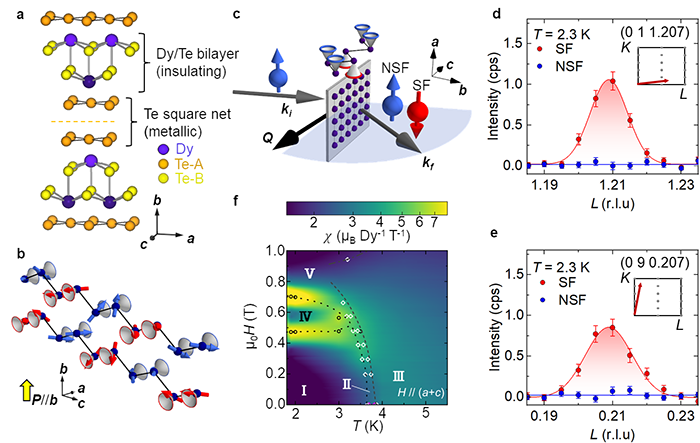
Non-coplanar helimagnetism in the layered van-der-Waals metal DyTe₃. a, Crystallographic unit cell with covalently bonded DyTe bilayers and metallic Te bilayers, with natural cleaving plane (dashed). b, Zigzag chain illustration of double-square net structure in DyTe₃. The interactions J₁, J₂ connect nearest and next-nearest neighbours in the zigzag chain model, respectively. Conical, noncoplanar helimagnetism is resolved in the zero-field ground state by neutron scattering. The cone direction, parallel to the a-axis, alternates both between pairs of magnetic sites in a zigzag chain, and between stacked zigzag chains. This texture causes polarization along the b-axis, i.e. perpendicular to square net bilayers (yellow arrow). c, Experimental geometry for polarized neutron scattering from layered DyTe₃ (grey plane, square net of Dy indicated). The scattering plane (blue) is spanned by wavevectors k_i, k_f of incoming and outgoing neutron beams, respectively. Separating spin-flip (SF, red) and non-spin flip (NSF, blue) scattering intensities at the detector, we identify conical magnetic order (top). d,e, Polarization analysis for the incommensurate cycloidal reflection q_cyc: absence of spin flip (SF) intensity indicates absence of mb and m_c, while non-spin flip (NSF) intensity reveals dominant m_a. f, Magnetic susceptibility χ for H∥[101], overlaid with phase boundaries from specific heat (white open circles) and magnetization (black circles): I (conical ground state), II, III, IV, and V.

Skyrmions in a centrosymmetric breathing Kagome magnet

Non-coplanar magnetic order in solids gives rise to an emergent magnetic field, which is known to strongly affect the motion of charge carriers. The magnitude of the emergent magnetic field is enhanced when pushing non-coplanar spin textures to shorter and shorter length scales λ. We have recently explored the limit of ultra-short range spin texture formation (λ~2-3 nanometers) in intermetallic magnets, where we found giant topological Hall and Nernst effects from non-coplanar skyrmion spin vortices. Hexagonal Gd₂PdSi₃ and Gd₃Ru₄Al₁₂ are centrosymmetric alloys which defy an important paradigm: typically, it is thought that Dzyaloshinskii-Moriya interactions arising exclusively in non-centrosymmetric material platforms are the key to skyrmion formation. Instead, competing interactions due to the high symmetry of the (hexagonal) lattice combine with Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions between Gd³⁺ rare earth moments to create a curious non-coplanar ordering on very short length scales. For example, the existence of the skyrmion lattice in Gd₃Ru₄Al₁₂ was confirmed by quantum beam (neutron & x-ray) scattering experiments as well as real-space imaging using Lorentz transmission electron microscopy (L-TEM), as shown in the figure. Future directions for skyrmions on centrosymmetric lattices are the exploration of new types of domains of left- and right-handed helicity, the coupling of the symmetry-breaking magnetic order to light, and the search for new types of magnetic vortex lattices, such as antiskyrmions or antiferromagnetically stacked skyrmions, due to the high level of spin-orientational degeneracy on the lattice. These exotic forms of magnetic order may be within reach in centrosymmetric magnets due to the flat energy landscape with many nearly degenerate magnetic states.

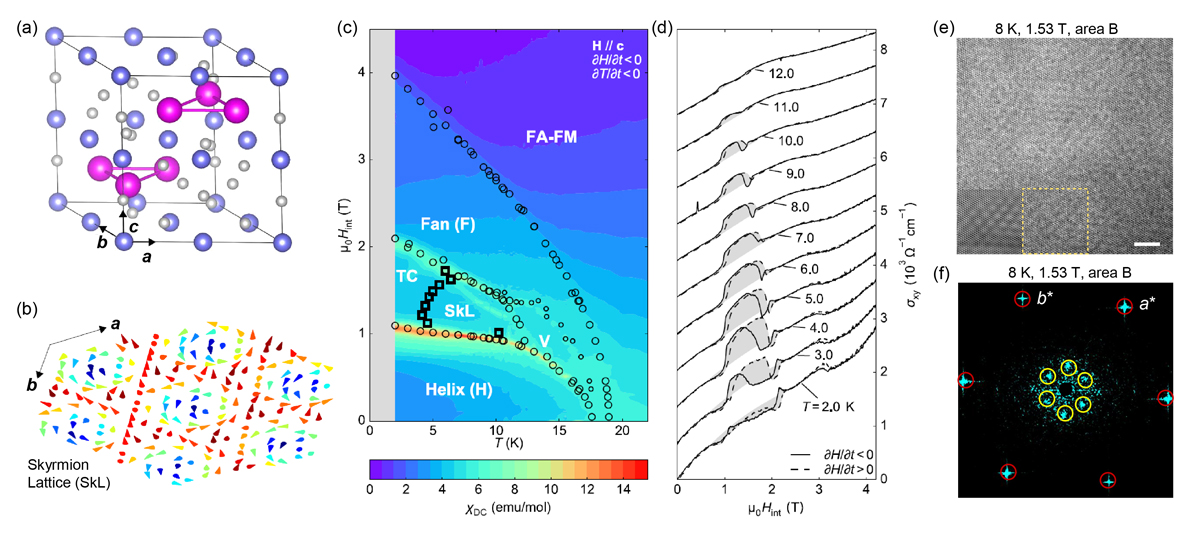
Skyrmion formation in the centrosymmetric hexagonal metal Gd₃Ru₄Al₁₂. (a) The crystal structure hosts closely correlated spin-trimers of Gd³⁺ moments, which are connected by weaker next-nearest neighbor interactions. The rare earth sites in each plane form a distorted (‘breathing’) Kagome network. (b) Illustration of a two-dimensional cut of the skyrmion spin vortex, with each cone representing an individual magnetic moment on a Gd-site of the lattice. (c) Magnetic phase diagram for field aligned along the c-axis, where many magnetic phases are observed due to competing interactions. (d) Only in the skyrmion lattice phase (labeled ‘SkL’) we found a large topological Hall signal, marked by grey shaded areas. (e) Real space image of a thin plate of Gd₃Ru₄Al₁₂ in phase SkL, where both the atomic lattice and the magnetic texture leave their fingerprints in the data. (f) Fourier transform of the data in panel (e), where reflections due to the atomic lattice and skyrmion spin textures are marked by red and yellow circles, respectively. Inset in (e) shows filtered data after removing intensity originating from the atomic lattice.